Soluţia propusă de Talmud la problema succesorală despre care am scris acum câteva zile nu este nici pe departe lipsită de logică. După ce, timp de sute de ani, exegeţii au încercat să-i găsească o explicaţie, matematicienii din a doua jumătate a secolului 20 au arătat că soluţia este nu doar coerentă, ci şi corectă.

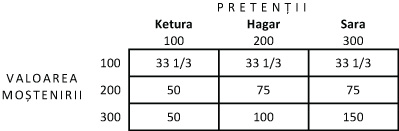
Cele trei soţii (să le zicem Ketura, Hagar şi Sara) au, fiecare, pretenţii de câte 100, 200 şi, respectiv, 300 de dinari. Vă reamintesc împărţirea propusă:

Pentru a înţelege principiul talmudic, trebuie să examinăm o problemă mult mai simplă. Tratatul Bava Metzia, al doilea tratat din cadrul “ordinului” Nezikin (Pagube), începe cu următoarea învăţătură:

Doi oameni ţin de o haină. […] Unul spune: “Toată e a mea”. Celălalt spune: “Jumătate e a mea”. […] Atunci primul va primi trei pătrimi [din valoarea ei], iar celălalt va primi o pătrime.

În teoria jocurilor, o ramură a matematicii zilelor noastre, acest tip de împărţire se numeşte “Diviziunea Egală a Sumei Contestate”. Cel de-al doilea pretendent nu contestă dreptul de proprietate al primului pretendent asupra a jumătate de haină. Prin urmare, această jumătate îi revine primului. Celalaltă jumătate rămâne în litigiu: ambii emit pretenţii asupra ei. În lipsa altor criterii de decizie, această jumătate se împarte în mod egal între cei doi pretendenţi.

Matematicienii Robert Aumann şi Michael Mashler au vrut să vadă în ce fel se aplică principiul “Diviziunii Egale a Sumei Contestate” (DESC) în cazul moştenirii buclucaşe. Cei doi au constatat că, în fiecare dintre cele trei cazuri, dacă se scade din masa succesorală oricare dintre moşteniri şi se împarte suma rămasă celorlalte două soţii, respectând principiul DESC, sumele rezultate sunt exact cele prevăzute în textul sacru.

E..g.: Dacă din 200 se scad 75 (Sara), Hagar şi Ketura au de împărţit 125. Ketura nu contestă dreptul lui Hagar asupra 25 de dinari (pretenţia ei e de doar 100). Suma contestată (100) se împarte la 2. Ketura primeşte 50 de dinari, Hagar 75.

Dacă din 300 se scad 50 (Ketura), Hagar şi Sara au de împărţit 250. Hagar nu contestă dreptul Sarei asupra 50 de dinari (pretenţia ei e de doar 200). Suma contestată (200) se împarte la 2. Hagar primeşte 100 de dinari, Sara 150.

Soluţia talmudică pare, aşadar, să respecte o condiţie de echitate. Mai mult, cei doi matematicieni au demonstrat că în orice situaţie în care o sumă trebuie împărţită între mai mulţi creditori cu pretenţii diferite există o soluţie care satisface principiul DESC şi numai una. Dar pentru a ajunge la această soluţie este nevoie de un procedeu matematic destul de complicat şi, cu siguranţă, inaccesibil autorilor textului talmudic.

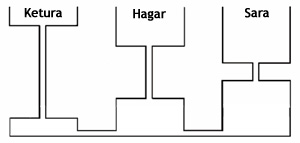
Aumann propune şi un procedeu empiric prin care aceste probleme pot fi rezolvate cu ajutorul unor vase comunicante. Imaginaţi-vă un vas al cărui volum este împărţit în două jumătăţi, separate de un capilar de capacitate neglijabilă. Construiţi acum trei vase al căror volum este egal cu pretenţiile celor trei soţii, astfel încât să aibă toate aceeaşi înălţime:

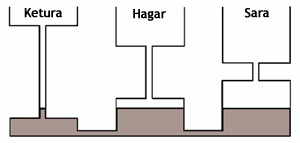
Dacă turnaţi în cele trei vase 100, 200, respectiv 300 litri de lichid, obţineţi exact împărţirea propusă de Talmud, care respectă principiul DESC:

Am dat peste această problemă fascinantă în cartea lui Len Fisher, Rock, Paper, Scissors: Game Theory in Everyday Life. Am găsit apoi articolul lui Robert Aumann, Game Theory in the Talmud, publicat în Jewish Law and Economics. Merită să-l parcurgeţi pentru alte exemple în care Talmudul aplică principiul “Diviziunii Egale a Sumei Contestate”. Articolul original al lui Aumann şi Mashler a fost publicat în Journal of Economic Theory 36 (1985, 195-213).

Tags: diviziune, diviziunea egala a sumei contestate, impartire, len fisher, litigiu, michael mashler, mostenire, robert aumann, sotii, succesiune, talmud, talmudul babilonian, teoria jocurilor